Decreasing Graph Complexity with Transitive Reductions

Graphs can contain a lot of unnecessary edges that make computations a lot more demanding. It is also harder to reason about the dependency structure of a graph with a lot of edges.

In the last guide, I implemented topological sorting and gave a basic introduction into what directed acyclic graphs (DAG) can be used for. In this post, we'll look at a technique called transitive reduction, first introduced Aho, Garey & Ullman in 1972.

A transitive reduction is a (sub-)graph of a given graph that meets two conditions:

there can only be a directed path from u to v in the transitive reduction if there is a directed path from u to v in the original graph.
there is no graph with fewer arcs than the transitive reduction satisfying the first condition

What this means in practice is that for a directed acyclic graph, there is one, and only one, transitive reduction.

And this issue is not just theoretical: Reducing graph complexity is a problem in software engineering in many areas, including Infrastructure-as-Code tooling like Terraform.

Example

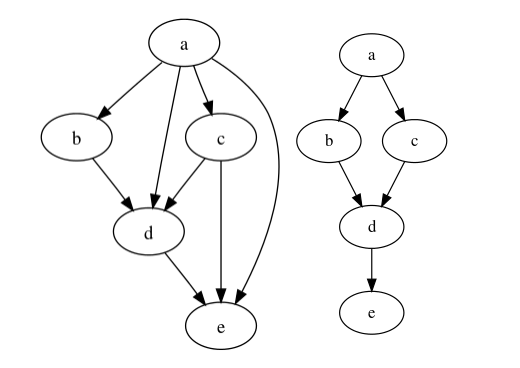
To make the concept of a transitive reduction more tangible, let's use the example provided in the Wikipedia article. The first graph below is the initial version with all dependencies. You can see that a has edges to b, c, d, and e. The edge to e is redundant since e also depends on c and b, which in turn depend on a. The same goes for the edge from a to d and from c to e.

The second image removes all redundant edges, it is the transitive reduction of the initial graph. As you can probably tell, the second graph is much easier to follow and reason about!

Implementing the transitive reduction algorithm

To create a transitive reduction, we must make sure that our graph does not contain cycles. An easy way to determine this is to use the topological sorting algorithm we implemented previously. This will throw an error in case of a cycle, which we can catch.

// detect if graph is acyclic
export function hasCycles<T>(input: Graph<T>) {
  try {
    topologicalSort(input);
    return false;
  } catch (e) {
    return true;
  }
}

Up next, we need to implement a depth-first traversal of our graph starting from any given node.

/**
 * Perform depth-first search on the graph
 * @param input Graph to perform DFS on
 * @param start start node
 * @param maxDepth if provided, will stop DFS at this depth
 * @returns
 */
export function dfs<T>(input: Graph<T>, start: T, maxDepth = Infinity) {
  const clonedGraph = new Graph<T>([...input.nodes], [...input.edges]);

  const visited: T[] = [];
  const stack: T[] = [start];

  // while stack is not empty
  while (stack.length > 0) {
    // remove a node n from stack
    const node = stack.pop();
    if (!node) {
      break;
    }

    // if n has not been visited then
    if (visited.includes(node)) {
      continue;
    }

    // add n to visited
    visited.push(node);

    // find all neighbouring nodes of node and push those we haven't visited
    for (const n of clonedGraph.nodesWithEdgeFromN(node)) {
      if (!visited.includes(n)) {
        stack.push(n);
      }
    }

    // if we reached max depth, stop walking
    if (visited.length >= maxDepth) {
      break;
    }
  }

  // cut off the starting node, we assume this is unique
  return visited.filter(v => v !== start);
}

To our Graph class, we need to add two more methods as well

countIncomingEdges(m: T) {
  return this.edges.filter(([_, to]) => to === m).length;
}

/**
 * Equivalent to indegree(G) of networkx
 * @returns
 */
countIncomingEdgesForNodes() {
  const nodeIncomingEdges = new Map<T, number>();

  for (const n of this.nodes) {
    nodeIncomingEdges.set(n, this.countIncomingEdges(n));
  }

  return nodeIncomingEdges;
}

With those two helper functions, we can get to implementing the actual transitive reduction.

ℹ️ Disclaimer: Due to a lack of available work on this algorithm, I ported the implementation from the popular NetworkX Python library.

/**
 * Performs transitive reduction on a given graph
 * (removes all unnecessary edges while maintaining the dependencies)
 *
 * This function is ported from networkx
 *
 * @param input
 * @returns
 */
export function transitiveReduction<T>(input: Graph<T>) {
  if (hasCycles(input)) {
    throw new Error('Graph has cycles');
  }

  // Start without any edges, this is important!
  const transitiveReduction = new Graph<T>([...input.nodes], []);

  const descendants: Map<T, Set<T>> = new Map();
  const checkCount: Map<T, number> = input.countIncomingEdgesForNodes();

  // Go over all nodes in the graph
  for (const u of input.nodes) {
    // Find neighbouring nodes of u
    const uNeighbours = new Set(input.nodesWithEdgeFromN(u));

    // Go over all neighbouring nodes (retrieve it once more since we'll modify uNeighbours)
    for (const v of input.nodesWithEdgeFromN(u)) {
      if (uNeighbours.has(v)) {
        if (!descendants.has(v)) {
          // Find descendants of v with depth-first search
          const walkedEdges = new Set(dfs(input, v));
          descendants.set(v, walkedEdges);
        }
        // Delete all descendants of v from uNeighbours
        for (const d of descendants.get(v)!) {
          uNeighbours.delete(d);
        }
      }

      checkCount.set(v, checkCount.get(v)! - 1);
      if (checkCount.get(v) === 0) {
        descendants.delete(v);
      }
    }
    // Add edges to our transitive reduction again
    for (const v of uNeighbours) {
      transitiveReduction.addEdge(u, v);
    }
  }

  return transitiveReduction;
}

Creating a transitive reduction

With everything in place and ready to use, let's make sure what we built and ported actually works. For this, we'll use the same example graph we talked about earlier.

const graph = new Graph();

graph.addNode('a');
graph.addNode('b');
graph.addNode('c');
graph.addNode('d');
graph.addNode('e');

graph.addEdge('a', 'b');
graph.addEdge('a', 'c');
graph.addEdge('a', 'd');
graph.addEdge('a', 'e');

graph.addEdge('b', 'd');

graph.addEdge('c', 'd');
graph.addEdge('c', 'e');

graph.addEdge('d', 'e');

const reduced = transitiveReduction(graph);

Running this code will yield the following value for reduced.edges:

[
  ["a", "b"],
  ["a", "c"],
  ["b", "d"],
  ["c", "d"],
  ["d", "e"]
]

This matches our initial assumptions and example transitive reduction.

That marks another guide on graph theory, admittedly we didn't build it all ourselves, but I think it's much more important to internalize the concepts and theory behind the applied solutions.